Unit 6 Similar Triangles Homework 2 Similar Figures Answer Key – A Guide to Mastery

Remember that daunting feeling of facing a stack of homework, especially when it involves geometry? I certainly do. For me, it was Unit 6, Similar Triangles, Homework 2: Similar Figures. It seemed like a maze of proportions and ratios, but with the right approach, it became much clearer. I learned that understanding the concepts, coupled with practice, were the keys to unlocking those seemingly complex problems. This blog post aims to provide you with the same clarity and confidence I gained, making your journey through similar figures a breeze.

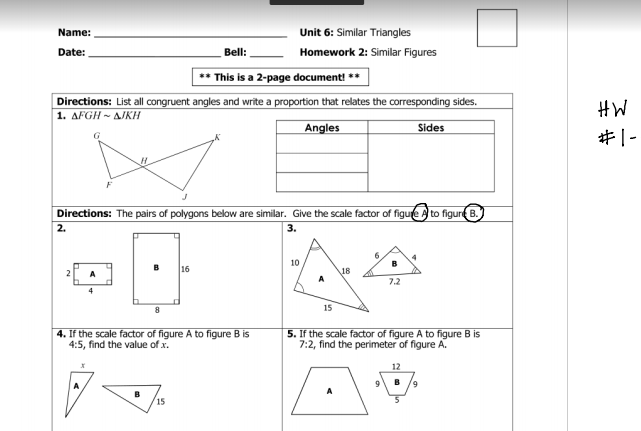
Image: www.chegg.com

This guide will equip you with the necessary tools to tackle your homework, gain a deeper understanding of similar figures, and conquer those challenging problems with confidence. We’ll delve into the fundamental concepts, explore real-world applications, and offer valuable tips and tricks to make your learning experience more effective.

Understanding Similar Figures: A Foundation for Success

Similar figures are like siblings – they resemble each other but differ in size. In geometry, this means that they have the same shape but different sizes. Think of two squares. They both have four right angles and four equal sides, but one might be smaller than the other. The key is that the corresponding angles of similar figures are equal, and their corresponding sides are proportional. This proportional relationship between sides is crucial to understand.

For instance, if you have two similar triangles, the ratio of any two corresponding sides of the smaller triangle to the larger triangle will be the same. Imagine a triangle with sides of 3 cm, 4 cm, and 5 cm. Now imagine a similar triangle with sides of 6 cm, 8 cm, and 10 cm. You’ll notice that the sides of the second triangle are twice as long as the corresponding sides of the first triangle. This consistent ratio is the fundamental principle behind similar figures.

Key Concepts of Similar Figures

1. Corresponding Sides and Angles

Similar figures have corresponding sides and angles. Corresponding sides are sides that occupy the same relative position in the figures, while corresponding angles are angles in the same relative position. The essence of similarity lies in the fact that corresponding angles are equal, while corresponding sides are proportional.

Image: www.coursehero.com

2. The Similarity Ratio

The similarity ratio is the ratio of corresponding side lengths of two similar figures. It is a vital tool for solving problems involving similar figures. To find the similarity ratio, choose any corresponding sides and divide their lengths. This ratio will be the same for all pairs of corresponding sides.

3. The Pythagorean Theorem

The Pythagorean theorem is a cornerstone of geometry and plays a significant role in working with similar figures. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem helps us solve for unknown side lengths in right triangles, which often arise in problems involving similar figures.

Let’s consider an example. Imagine you have two similar right triangles. You know the length of one leg of the smaller triangle and the length of the hypotenuse of the larger triangle. Using the similarity ratio, you can find the corresponding sides of the larger triangle. Then, apply the Pythagorean theorem to solve for the unknown leg of the larger triangle.

Unit 6 Similar Triangles Homework 2: Similar Figures Answer Key

Unit 6 Similar Triangles Homework 2 often includes exercises that require you to determine if figures are similar, find the similarity ratio, and solve for unknown side lengths. To tackle these problems efficiently, remember these key steps:

1. Identify Corresponding Sides and Angles: Identify the sides and angles that correspond in the given figures.
2. Check for Equal Corresponding Angles: Ensure that all corresponding angles are equal.
3. Check for Proportional Corresponding Sides: Verify that the ratios of corresponding sides are equal.
4. Use the Similarity Ratio: If the figures are similar, determine the similarity ratio by dividing the length of any corresponding side from one figure by the length of the corresponding side from the other figure.
5. Solve for Unknown Side Lengths: Use the similarity ratio and the Pythagorean theorem to solve for any missing side lengths.

Tips and Expert Advice on Unit 6 Similar Triangles Homework 2

Mastering Unit 6 Similar Triangles Homework 2 requires more than just understanding the concepts; it demands strategic approaches and practice.

1. Practice Makes Perfect

Practice is essential. The more you work with similar figures, the better you’ll become at identifying them, understanding their properties, and solving problems related to them. Complete all the problems in your textbook and seek out additional practice problems online or in your study material.

2. Visualize and Draw

Visual aids can help tremendously. When tackling a problem, draw the figures and label the corresponding sides and angles. Visualizing the figures can make it easier to identify the crucial relationships and apply the concepts of similarity.

3. Break Down Complex Problems

If a problem seems overwhelming, break it down into smaller, manageable steps. Focus on identifying the key information, applying the relevant concepts, and solving for the unknowns one at a time. Don’t be afraid to work through each step methodically.

FAQs about Unit 6 Similar Triangles Homework 2

Q1. What are the applications of similar figures in real life?

Similar figures have many applications in real life, such as:

• Mapping and Surveying: Maps are scaled-down representations of real-world locations, utilizing the principles of similar figures.
• Architecture and Design: Architects and designers use similar figures to create scaled models of buildings and structures, ensuring proportions are maintained.
• Photography: Cameras use lenses to create images that are similar to the original scene, but scaled down.

Q2. How can I check if two figures are similar?

To determine if two figures are similar, check the following:

• Equal Corresponding Angles: All corresponding angles must be equal.
• Proportional Corresponding Sides: The ratios of all corresponding sides must be equal (the same similarity ratio).

Q3. What happens if figures have equal corresponding angles but their corresponding sides are not proportional?

If figures have equal corresponding angles but their corresponding sides are not proportional, they are not similar. They may have the same shape but not the same size, which is a key requirement for similarity.

Unit 6 Similar Triangles Homework 2 Similar Figures Answer Key

Conclusion

Mastering Unit 6 Similar Triangles Homework 2 requires a combination of understanding the core concepts, applying the techniques, and practicing diligently. By delving into the fundamentals of similar figures, utilizing effective strategies, and seeking help when needed, you can confidently tackle those challenging problems and achieve a deep understanding of this important geometric concept. This guide has provided you with the tools and tips to navigate this unit with success. Remember, practice is key, and understanding the principles behind the problems will make the entire process more enjoyable.

Are you interested in exploring more advanced applications of similar figures? Let us know in the comments below, and we can delve further into this fascinating world of geometry!