Unraveling the Mystery – Parallel Lines and Transversals in 2-7 Practice

Have you ever looked at a street grid and wondered how those seemingly endless parallel lines interact with the crisscrossing diagonal streets? This intricate dance of lines is a fundamental concept in geometry, and it’s the very foundation of understanding angles, shapes, and patterns that surround us. Welcome to the fascinating world of parallel lines and transversals, where a single line can unleash a cascade of corresponding, alternate interior, and alternate exterior angles.

Image: www.pinterest.com.au

This exploration delves into the heart of 2-7 practice, where we’ll unlock the secrets of these powerful geometric relationships. Understanding parallel lines and transversals isn’t just about passing a math test, it’s about developing a deeper appreciation for the structure that underpins the world around us. From the design of buildings to the intricate pathways of a spider’s web, these concepts are woven into the very fabric of our reality.

Laying the Foundation: Parallel Lines

Definition and Properties

Imagine two railway tracks stretching out into the horizon. They never intersect, always maintaining an equal distance apart. This visual representation embodies the essence of parallel lines. In geometry, parallel lines are defined as two or more lines that lie within the same plane and never intersect. They are like two companions walking side-by-side, their paths never crossing, no matter how far they journey.

Symbolism: The Double Arrow

To visually represent parallel lines, we use a special symbol: a double-headed arrow. When you see this arrow placed above two lines, it’s a clear indication that those lines are parallel. This simple symbol serves as a shorthand code, allowing us to quickly identify and understand the relationship between lines.

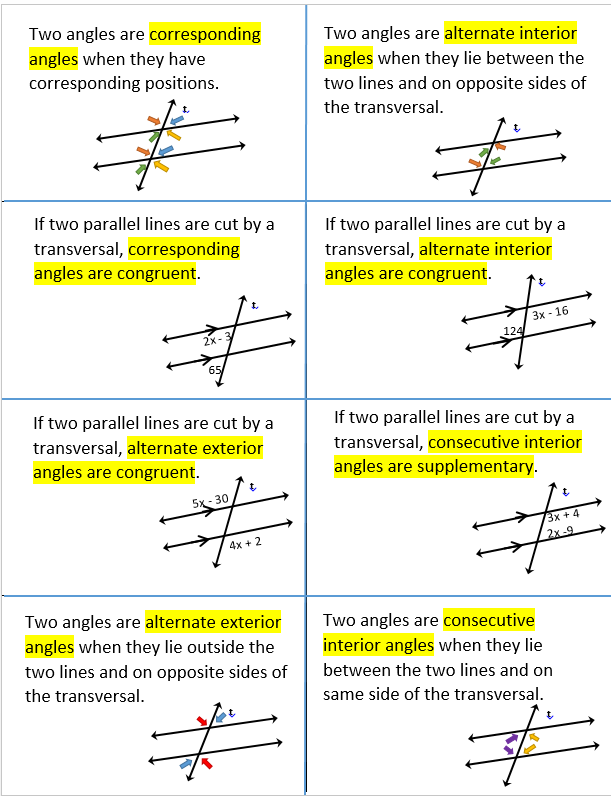
Image: materiallistholtzmann.z1.web.core.windows.net

Introducing the Intertwiner: The Transversal

Now, imagine a road cutting across those railway tracks. This road is your transversal. A transversal is a line that intersects two or more parallel lines. It acts as a bridge, connecting these parallel lines and creating a fascinating interplay of angles in the process.

The Importance of the Angle

It’s within this interaction that the magic unfolds. The transversal divides the parallel lines into distinct angles. Angles formed on the same side of the transversal, either between the parallel lines or outside, are called corresponding angles. Imagine those angles as mirrored reflections, sharing properties of measure and position.

A World of Angle Pairs

The transversal creates other intriguing pairs: alternate interior angles, situated inside the parallel lines on opposite sides of the transversal, and alternate exterior angles, found outside the parallel lines on opposite sides. These angles are also equal in measure, like two dancers executing synchronized steps.

The Power of Parallel Lines and Transversals

From Proofs to Real-World Applications

The concepts of parallel lines and transversals are not confined to the realm of pure theory. They have powerful applications in many fields.

• Engineering and Architecture: Construction of bridges, buildings, and other structural marvels relies heavily on the understanding of parallel lines and transversals. This ensures stability and strength. Think of the parallel beams supporting the weight of a bridge, or the precise alignment of columns in a building. These applications ensure stability and strength.
• Navigation and Surveying: Ships navigating the vast oceans and surveyors meticulously mapping land use these geometrical concepts to determine accurate positions and directions. The alignment of stars and celestial bodies, for instance, relies on the principles of parallel lines and transversals. These concepts guide us across the Earth and beyond.
• Art and Design: Artists and designers utilize parallel lines and transversals to create visual harmony, depth, and perspective. Think of the parallel lines converging at a distant point to create the sense of perspective in a painting. From intricate patterns in textiles to the balanced composition of a photograph, these concepts play a vital role in visual aesthetics.

2-7 Practice: Unlocking the Relationship

In the context of 2-7 practice, we delve deeper into the relationships between these angles. One of the key principles to grasp is that corresponding angles are equal, as are alternate interior angles and alternate exterior angles. This understanding forms the basis for solving problems and proving geometric theorems.

Example: Solving for Unknown Angles

Imagine a diagram with two parallel lines intersected by a transversal. You might be asked to find the measure of an unknown angle. By applying the principles of corresponding angles, alternate interior angles, or alternate exterior angles, you can deduce the unknown angle measure through logical reasoning.

For example, if you’re given that one corresponding angle measures 70 degrees, you can immediately conclude that the other corresponding angle also measures 70 degrees. This seemingly simple concept opens up a world of problem-solving opportunities.

Beyond the Textbook: A Glimpse into Higher Math

The concepts of parallel lines and transversals serve as a foundation for more complex geometric topics. In higher math, you’ll encounter concepts like similar triangles and trigonometric functions, where the understanding of angles and their relationships is crucial to understanding these more advanced ideas.

2-7 Practice Parallel Lines And Transversals

Conclusion: A Journey of Understanding

Embarking on the journey of understanding parallel lines and transversals is like venturing into a new dimension of geometric knowledge. From the basic definition of parallel lines to the intricate relationships formed by transversals, each step reveals a deeper understanding of the world around us. Don’t just limit yourself to memorizing formulas; explore the visual patterns, delve into the real-world applications, and allow your curiosity to guide you through this fascinating geometric landscape. The world is full of parallel lines and transversals, waiting to be discovered and understood. Go forth and unlock their secrets.