Unraveling the Magic of Linear Equations – A 2, 4, Practice Guide

Have you ever wondered how everyday phenomena, such as calculating the cost of groceries or predicting the distance traveled by a car, can be neatly summarized by a simple equation? This is the power of linear equations, mathematical expressions that describe a direct relationship between two variables. From charting your progress on a fitness journey to understanding the intricacies of economics, linear equations are the invisible threads weaving through countless aspects of our lives. This guide will delve into the fascinating world of linear equations, offering a practical and engaging path to mastering this fundamental mathematical concept.

Image: materiallistfried.z19.web.core.windows.net

Imagine a scenario where you’re trying to calculate the total cost of a pizza delivery. The base price of the pizza is $10, and each additional topping costs $1. How can you determine the final cost for any number of toppings? This seemingly simple problem can be elegantly solved with a linear equation. By representing the number of toppings with the variable ‘x’ and the total cost with the variable ‘y’, we can write the equation as: y = 10 + 1x. This equation perfectly captures the relationship between the cost and the number of toppings, allowing us to swiftly calculate the final price for any pizza order.

Demystifying Linear Equations: The Building Blocks of Understanding

Linear equations are like a puzzle, with each piece representing a distinct element that contributes to the overall picture. One of the fundamental concepts is the slope, which represents the rate of change in the dependent variable (y) with respect to the independent variable (x). For instance, in our pizza example, the slope is 1, indicating that the price increases by $1 for each additional topping. This constant rate of change is a defining characteristic of linear relationships.

Another crucial element is the y-intercept, which is the point where the line intersects the y-axis. In our example, the y-intercept is 10, representing the base price of the pizza even without any toppings. Visualizing the equation as a line on a graph can provide a powerful intuitive understanding. The slope determines the steepness of the line, while the y-intercept indicates the point where the line crosses the vertical axis.

The Power of Solving: Unveiling the Unknown

Linear equations are not merely descriptive; they are powerful tools for solving problems and finding unknown values. These solutions are often represented as ordered pairs (x, y), where each point on the line satisfies the equation. The most common techniques for solving linear equations include:

• Substitution Method: This method involves isolating one variable in terms of the other and then substituting it into the other equation. This results in a single equation with one variable, which can then be solved.
• Elimination Method: This technique involves manipulating the equations by multiplying them by constants to eliminate one of the variables. The remaining equation can then be solved to find the value of the other variable.

2, 4, Practice: A Journey Towards Mastery

To truly grasp the essence of linear equations, practice is paramount. Here are a few exercises that will help you hone your skills and unlock the power of these mathematical expressions:

1. Graphing Linear Equations: Take various linear equations and plot them on a graph. Observe the slope and y-intercept of each line, and analyze the relationship between the variables. Pay close attention to how the slope affects the steepness of the line. This visual approach will deepen your understanding of how equations translate into practical representations.

2. Solving Systems of Linear Equations: Practice solving systems of two or more linear equations using the substitution or elimination methods. Mastering these techniques will enhance your ability to find solutions where multiple equations intersect. These solutions represent the points where all equations are satisfied simultaneously.

3. Word Problems: Translate real-world scenarios into linear equations and then solve them. For example, you can model situations involving travel expenses, rental costs, or even the growth of a plant over time. Applying linear equations to practical contexts will solidify your understanding and demonstrate their value in everyday life.

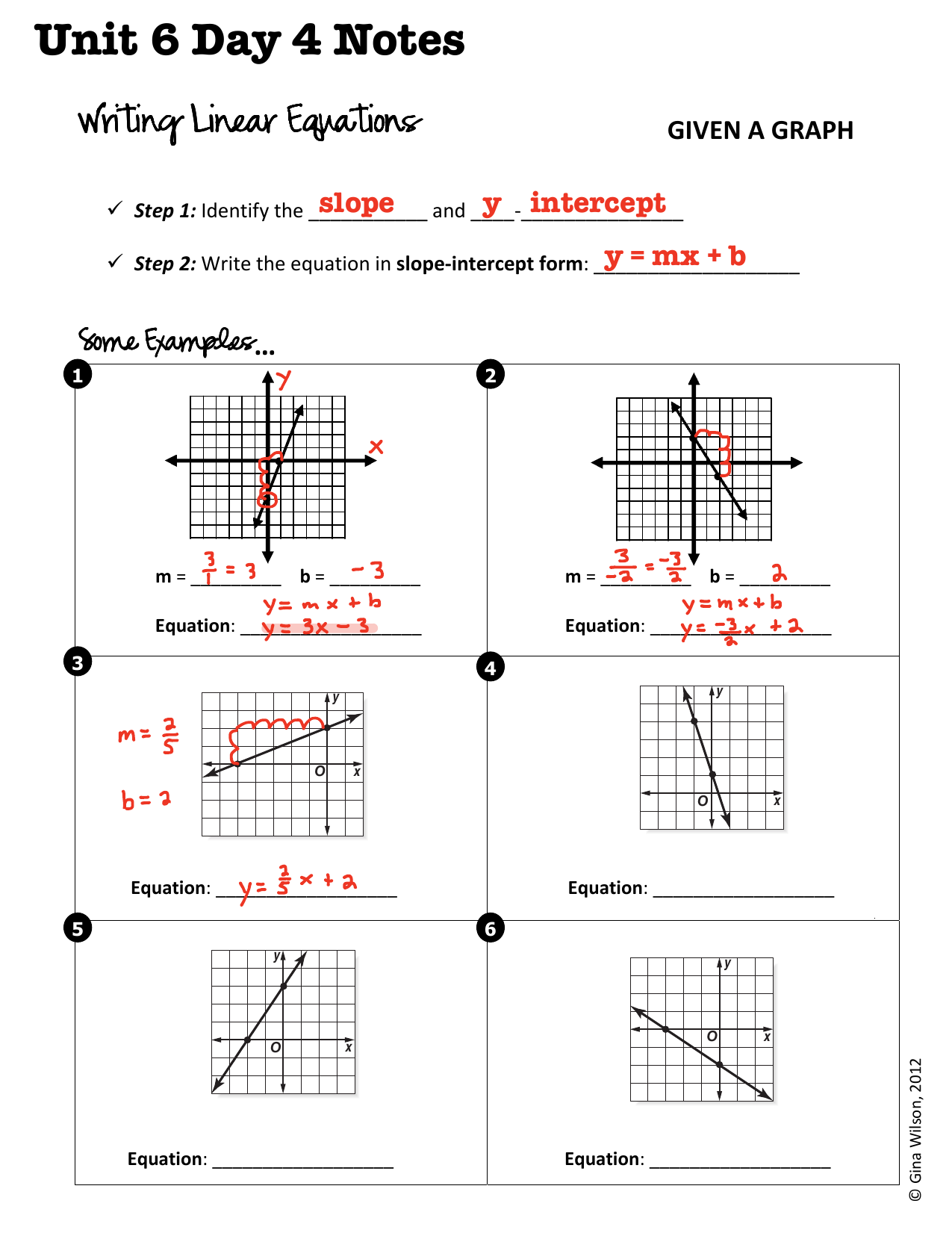
Image: www.abhayjere.com

Expert Insights: Unlocking the Potential of Linear Equations

“Linear equations form the foundation of many advanced mathematical concepts”, says Professor Sarah Jones, a renowned mathematician at Stanford University. “Understanding their structure and properties is essential for tackling complex problems in fields like physics, engineering, and economics.”

“Don’t be intimidated by the term ‘linear equations’ “, advises Dr. David Lee, a physics professor at MIT. “Think of them as tools for unraveling patterns and relationships in the world around us. With practice, you’ll be able to see the world through the lens of these elegant mathematical expressions.”

2 4 Practice Writing Linear Equations

Embrace the Journey: A Call to Action

Linear equations are more than just a chapter in a math textbook; they are vital tools for understanding and navigating the complex world around us. From predicting weather patterns to designing robots, linear equations are interwoven through the fabric of modern civilization. By devoting time to practice and engaging with real-world applications, you can unveil the power of linear equations and unlock your potential to solve problems and make informed decisions. Share your experiences in the comments below, and let’s continue the journey of exploring and appreciating the beauty and practicality of linear equations together!