Remember that frustrating moment in geometry class when you just couldn’t grasp the concept of perpendicular bisectors and angle bisectors? It seemed like a maze of lines and angles, leaving you feeling lost in a sea of mathematical jargon. Well, fear not! This guide is here to break down the intricacies of perpendicular and angle bisectors, making them as clear as day. We’ll explore the definition, properties, and applications of these essential geometric concepts, armed with a comprehensive explanation of the key terms and visual representations. Get ready to conquer those geometry problems with confidence!
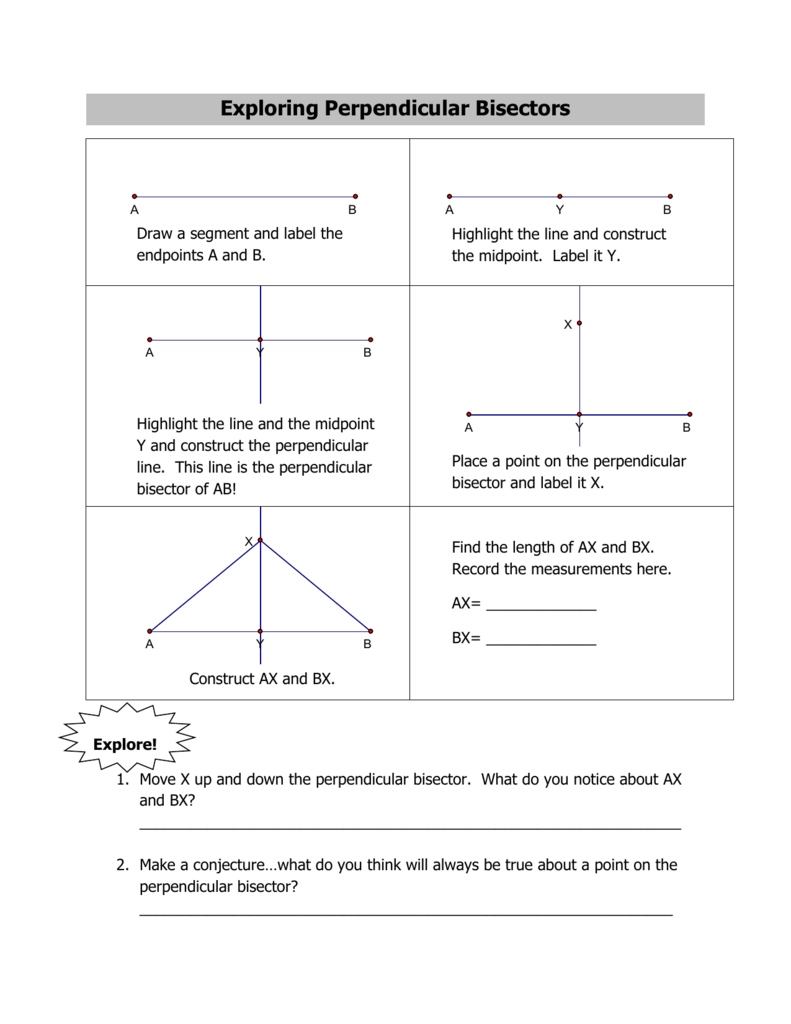
Image: manualfixfaber.z19.web.core.windows.net
Let’s imagine you’re trying to find the center of a circular pizza. You might instinctively grab a ruler and draw a line across the pizza, then draw another line perpendicular to the first one. The point where these lines intersect – that’s the center of your pizza, which is also the center of the circle! This is the magic of perpendicular bisectors. They can help us locate the midpoint of a line segment and, in this case, the center of a circle. But what about angle bisectors? These lines divide an angle into two equal parts. Let’s say you’re building a house and need to precisely split a corner angle to ensure symmetry. That’s where angle bisectors come in, providing the perfect solution.
Understanding “5.1 Perpendicular and Angle Bisectors”
The phrase “5.1 Perpendicular and Angle Bisectors” usually refers to a chapter or section in a geometry textbook that delves into the properties and applications of these fundamental geometric concepts. It often includes a combination of definitions, theorems, examples, and practice problems. Within this context, a “5.1 Perpendicular and Angle Bisectors Answer Key PDF” would be a supplemental document providing the solutions to the practice problems found in that chapter.
Perpendicular bisectors and angle bisectors play a crucial role in various geometric principles and constructions. These are not just theoretical ideas; they have real-world applications in fields like architecture, engineering, and even art, where precision and symmetry are essential. Understanding these concepts is fundamental to grasping more complex geometric theorems and tackling a wide range of problems.
Exploring the World of Perpendicular Bisectors
Definition
A perpendicular bisector is a line that passes through the midpoint of a line segment and is also perpendicular to that segment. It essentially cuts the line segment into two equal parts, forming right angles at the point of intersection.

Image: afiqkarimduaaa.blogspot.com
Properties
Perpendicular bisectors have several important properties that make them so valuable in geometric constructions. Firstly, any point on the perpendicular bisector is equidistant from the endpoints of the line segment. This means that the distance from the point to one endpoint of the segment is equal to the distance from that point to the other endpoint. This property is crucial in locating the center of a circle, as all points on the circle are equidistant from the center.
Applications
Perpendicular bisectors have numerous practical applications. As mentioned earlier, they are used to find the center of a circle. This is fundamental in constructing circles, determining the radius, and understanding their properties. In addition, perpendicular bisectors are essential in dividing line segments into equal parts, creating symmetrical shapes, and proving geometric relationships. They also play a key role in constructions like compass and straightedge constructions, where they are used to divide line segments, create perpendicular lines, and construct triangles.
Unraveling the Secrets of Angle Bisectors
Definition
An angle bisector is a line or ray that divides an angle into two congruent angles, meaning they have equal measures. It essentially splits the angle precisely in half.
Properties
Angle bisectors possess important properties. Any point on the angle bisector is equidistant from the sides of the angle. This means that the distance from the point to one side of the angle is equal to the distance from the point to the other side. This property is useful in proving geometric relationships and constructing congruent angles.
Applications
Angle bisectors are used in constructing congruent angles, dividing angles into equal parts, and creating symmetrical shapes. They are also crucial in solving problems involving triangles, such as finding the incenter of a triangle, which is the point where all three angle bisectors intersect. The incenter has the unique property of being equidistant from all three sides of the triangle. Furthermore, angle bisectors are used in various applications like construction, surveying, and creating artistic designs.
5.1 Perpendicular and Angle Bisectors Answer Key PDF: A Useful Resource
The 5.1 Perpendicular and Angle Bisectors Answer Key PDF is an indispensable tool for students studying geometry. It provides the solutions to the practice problems presented in the corresponding chapter, allowing students to check their work and identify any areas where further clarification and practice are needed. It acts as a guide, helping students develop a deeper understanding of the concepts and the ability to apply them to different situations.
By utilizing the answer key, students can:
- Confirm their understanding of the definitions and properties of perpendicular bisectors and angle bisectors.
- Analyze the steps involved in solving various problems related to perpendicular bisectors and angle bisectors.
- Identify and correct any misconceptions or mistakes they might have made while solving problems.
- Gain a stronger foundation in geometric concepts, preparing them for more advanced topics in geometry and other related subjects.
Tips and Expert Advice
Here are some tips from expert geometry instructors to make the most of your learning experience with perpendicular bisectors and angle bisectors:
- Start with the basics: Make sure you have a solid understanding of the definitions and terminology related to these concepts. Memorizing the key properties will help you apply them in different contexts.
- Engage in active learning: Don’t just read through the textbook. Solve plenty of practice problems, create your own diagrams, and try to visualize the concepts in action.
- Visualize the concepts: Draw diagrams to represent the problems and use different colored pencils to highlight perpendicular lines, angle bisectors, and other key elements. This can help you understand the relationships between different components.
- Connect the concepts to real-world applications: Look for examples of perpendicular bisectors and angle bisectors in the world around you. This will make the concepts more relatable and easier to memorize.
- Utilize online resources: There are numerous online resources that can help you learn and practice geometric concepts. Websites, videos, and interactive simulations can provide a different perspective and make learning more engaging.
FAQ: Perpendicular Bisectors and Angle Bisectors
Q: What is the difference between a perpendicular bisector and an angle bisector?
A: A perpendicular bisector cuts a line segment in half at a right angle, while an angle bisector divides an angle into two equal angles.
Q: What are some real-world examples of perpendicular bisectors and angle bisectors?
A: Perpendicular bisectors are used in constructing buildings, designing bridges, and creating symmetrical shapes in art. Angle bisectors are used in dividing land, creating angles in architecture, and constructing equal angles in carpentry.
Q: How can I find the perpendicular bisector of a line segment?
A: You can find the perpendicular bisector of a line segment by:
- Using a compass and straightedge to construct the bisector.
- Finding the midpoint of the line segment and drawing a line perpendicular to that point.
- Using a compass and straightedge to construct the bisector.
- Drawing two arcs of equal radius from the vertex of the angle. The line segment connecting the vertex to the point where the arcs intersect is the angle bisector.
Q: How can I find the angle bisector of an angle?
A: You can locate the angle bisector of an angle by:
5.1 Perpendicular And Angle Bisectors Answer Key Pdf
Conclusion
Perpendicular bisectors and angle bisectors are fundamental concepts in geometry with numerous practical applications. Understanding these concepts is essential for success in geometric problems and for applying geometric principles to real-world scenarios. Whether you’re a student struggling to grasp the definitions or an adult looking to refresh your geometry knowledge, this article provides a comprehensive guide, tips, and even a FAQ section to help you navigate the world of perpendicular bisectors and angle bisectors. Are you ready to conquer the challenges of geometry and unlock the secrets of these fascinating geometric concepts?



![Cyclomancy – The Secret of Psychic Power Control [PDF] Cyclomancy – The Secret of Psychic Power Control [PDF]](https://i3.wp.com/i.ebayimg.com/images/g/2OEAAOSwxehiulu5/s-l1600.jpg?w=740&resize=740,414&ssl=1)

