Remember that moment in elementary school when you first encountered the concept of place value? It felt like a magical equation unlocking a whole new world of numbers. From single digits to multi-digit numbers, the system seemed intricate yet undeniably crucial to understanding how numbers work. Today, we’re going to take a trip down memory lane and explore the fascinating world of place value – revisiting its basics and uncovering its foundational role in mathematics.

Image: guidedmath.expert
If you’re struggling with place value, you’re not alone. Many students find it confusing at first. However, once you grasp the fundamental principles, it becomes a breeze! This article will guide you through the concepts, unraveling the mysteries behind place value and empowering you to confidently tackle your homework assignments.
What is Place Value?
Place value is the concept that the position of a digit in a number determines its worth. It is like a numerical address system, each digit occupying a specific slot with an assigned value. For instance, consider the number 123. The digit 1 is in the hundreds place, indicating a value of 100; the digit 2 is in the tens place, reflecting a value of 20; and the digit 3 is in the ones place, signifying a value of 3. Every digit in a number plays a distinct role, contributing its specific value to the overall representation.
Place value is not just a theoretical concept; it’s a fundamental principle that underpins our understanding of numbers and essential for performing various mathematical operations. From addition and subtraction to multiplication and division, every arithmetic process relies on our ability to identify and utilize place values within a number.
Unveiling the Number System: A Glimpse into Place Value
The Building Blocks of Numbers
The foundation of our number system is the decimal system, based on ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These digits are like the building blocks of all the numbers we work with. The decimal system is called “base-ten” because each place value represents a power of ten. Starting from the rightmost digit, the places are units (10⁰), tens (10¹), hundreds (10²), thousands (10³), and so on.
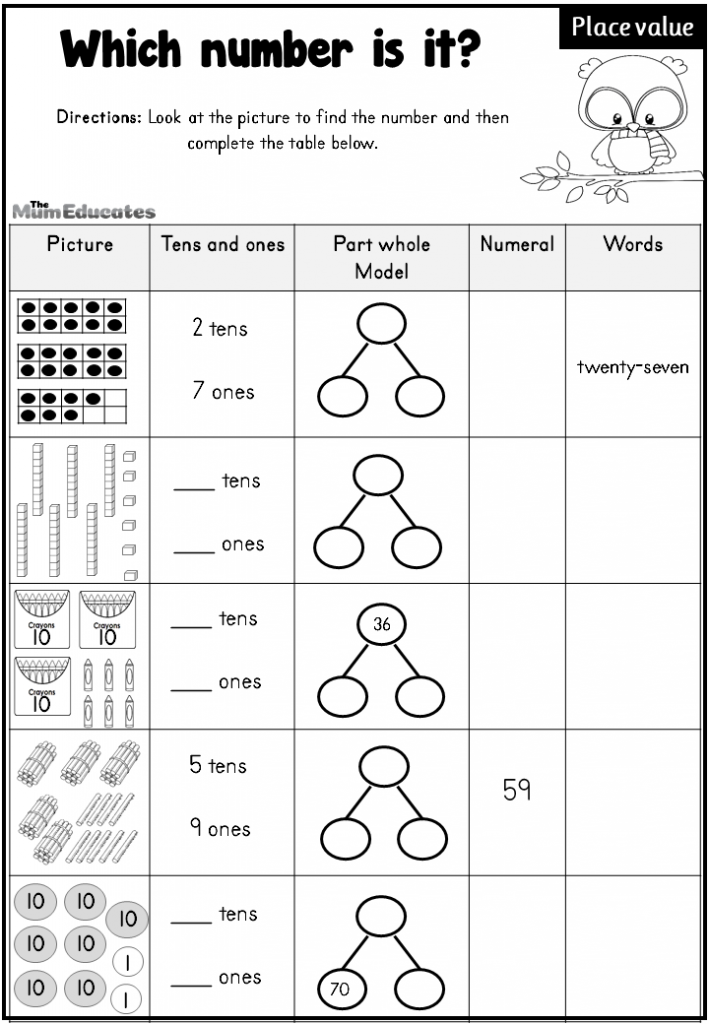
Image: www.animalia-life.club
Visualizing Place Value: Understanding the Power of Ten
Imagine a box with multiple compartments. Each compartment represents a place value, and within each compartment, we place a digit. For example, for the number 2,485, we would put the digit 2 in the thousands compartment, the digit 4 in the hundreds compartment, the digit 8 in the tens compartment, and the digit 5 in the ones compartment. The arrangement of the digits within these compartments reflects their respective place values.
The Power of Ten: Exponents in Place Value
Place values are essentially powers of ten. The ones place represents 10⁰ (which is 1), the tens place represents 10¹, the hundreds place represents 10², and so on. The exponent of ten indicates the number of times ten is multiplied by itself. For example, 10² is 10 x 10, which equals 100. This means the digit in the hundreds place holds a power of ten squared.
The Role of Zero: A Place-Holder
In a number system, the digit 0 holds a valuable role as a placeholder. It signifies the absence of a value in a specific place. For example, consider the number 602. The 0 in the tens place shows that there’s no digit in that place, highlighting that the number only contains a value in the hundreds and units place.
Understanding Place Value Through Real-World Applications
Money: A Practical Illustration of Place Value
Consider a currency system that uses coins and bills. Each denomination, like a penny, a dime, a dollar, or a ten-dollar bill, represents a specific place value. When you combine different denominations, their individual values add up based on their respective place values to determine the total amount of money. Imagine having 1 dollar, 2 dimes, and 5 pennies. You can visually relate this to the place value concept, where the dollar bill represents the hundreds place, the dimes represent the tens place, and the pennies represent the ones place.
Time: Another Familiar Example
Our time system also utilizes the place value concept. In a standard twelve-hour clock, the hour and minute hands represent different place values. The hour hand corresponds to the tens place, while the minute hand corresponds to the ones place. For instance, 3:15 represents three hours (3 tens) and fifteen minutes (15 ones).
Applying Place Value to Solve Math Problems
Addition and Subtraction: Essential Operations
Place value plays a vital part in performing addition and subtraction. We align numbers vertically so that digits with the same place values are aligned in the same columns. For example, when adding 235 and 142, we place the digits in their corresponding columns – the hundreds, tens, and ones. We then add the digits in each column, carrying over any excess to the next column if the sum exceeds nine.
Multiplication: Building upon Place Value
Multiplication also heavily relies on place value. The product of each digit in the multiplicand is determined by its place value and multiplied with the multiplier. For example, multiplying 12 by 3 involves multiplying 2 (ones place) by 3, and then multiplying 1 (tens place) by 3, finally adding the products accordingly.
Division: A Balancing Act with Place Value
Division is a process of repeated subtraction, and place value is instrumental in understanding the quotient and remainder. We divide the dividend by the divisor, looking at the place values of the dividend to determine how many times the divisor fits into it. The result of each step involves understanding the place value of the quotient and the remainder.
Place Value: A Foundation for Mathematical Proficiency
Beyond Basic Arithmetic: The Power of Place Value
As we delve deeper into mathematics, the understanding of place value becomes increasingly crucial. From understanding fractions, decimals, and exponents to grasping more complex concepts like algebra, geometry, and calculus, the foundation of place value remains indispensable.
Unlocking Higher-Level Mathematical Concepts
Imagine tackling a complex algebraic equation. You need to manipulate variables and coefficients, understanding their corresponding place values. You might encounter exponents and decimals, and successfully managing these complex expressions hinges on your understanding of place value. The principles learned in elementary school continue to be instrumental as we progress in mathematics, solidifying a comprehensive understanding of numerical relationships and operations.
Place Value: A Tool for Everyday Life
Place value is not just confined to textbooks and classrooms. It is a vital tool for daily life, enabling us to manage finances, make informed decisions, and navigate our world effectively. From balancing your budget to understanding interest rates, place value is an essential skill for everyone.
Beyond the Classroom: Making Informed Decisions
Understanding place value empowers us to make informed financial decisions. For instance, recognizing place values in loan terms can help you assess interest rates and repayment options. Understanding place value in pricing comparisons enables you to make smart choices for purchases. It’s a skill that transcends the classroom, becoming a valuable asset in our daily lives.
Place Value: A Foundation for Future Success
Developing a Strong Foundation for Future Mathematical Success
The concepts of place value learned in the early stages of education serve as a fundamental foundation for future mathematical learning. A strong grasp of place value provides a solid base from which to explore more advanced topics. It fosters an understanding of number systems, numerical relationships, and mathematical operations. Building a strong understanding of place value at an early age sets the stage for success in mathematics throughout your academic journey.
A Gateway to Advanced Mathematical Concepts
As you progress to higher-level mathematics, the foundation of place value remains critical. It empowers you to tackle complex equations, analyze data, and explore intricate mathematical concepts. Place value is a foundational element, a gateway to unlocking the vast landscape of mathematical possibilities.
FAQ
Q: What are the main uses of place value?
A: Place value is fundamental to our understanding of numbers and forms the basis for various mathematical operations such as addition, subtraction, multiplication, and division. It is also essential for understanding decimals, fractions, and more complex mathematical concepts.
Q: How do I teach place value to a young learner?
A: Use hands-on activities like using manipulatives (blocks, counters, etc.) to represent place values. Create visual aids like place value charts. Use real-world examples like money (different denominations of coins and bills) to illustrate the concept.
Q: What are some common mistakes learners make with place value?
A: Learners may misalign numbers during mathematical operations, causing errors in addition or subtraction. They may struggle to understand the concept of zero as a placeholder. Additionally, they may confuse the value of a digit with its place value. These issues can be addressed by using visual aids, hands-on activities, and practicing regularly.
My Homework Lesson 1 Place Value
Conclusion
Understanding place value is vital for mathematical success in both elementary and higher education. It’s not just about memorizing digits or manipulating numbers but understanding the underlying system that powers our comprehension and use of numbers. From basic arithmetic to advanced mathematical concepts, the power of place value remains a fundamental cornerstone. Are you ready to embrace the fascinating world of place value?



![Cyclomancy – The Secret of Psychic Power Control [PDF] Cyclomancy – The Secret of Psychic Power Control [PDF]](https://i3.wp.com/i.ebayimg.com/images/g/2OEAAOSwxehiulu5/s-l1600.jpg?w=740&resize=740,414&ssl=1)

